Ueber barometrisches Höhenmessen
Mit besonderer Berücksichtigung des Hochgebirges.
Dr. C. Koppe.
" Von Bei der mannigfachen Anwendung, welche die barometrischen Höhenmessungen namentlich seit Erfindung und Verbesserung der Aneroïdbarometer gefunden haben, dürfte es wohl nicht unangemessen erscheinen, die Grundlagen, auf welchen solche Messungen beruhen, einmal etwas näher in 's Auge zu fassen, um darüber klar zu werden, welche Genauigkeit der Höhenbestimmung auf diesem Wege erreicht werden kann und welche Methode je nach den speziellen Umständen die günstigsten Resultate zu liefern im Stande ist; eine Frage, über welche sehr verschiedene Ansichten herrschen, die aber bei solchen Höhenunterschieden, wie sie in den Alpen vorkommen, nicht unberücksichtigt bleiben darf, wenn man genaue Resultate erreichen will.
Beim Barometer hält bekanntlich eine Quecksilbersäule einer gleich schweren Luftsäule das Gleichge- gewicht, beim Anéroïde hingegen ist die Quecksilbersäule durch die elastische Kraft einer Peder ersetzt, die, je nachdem die Luftsäule schwerer oder leichter wird, sich zusammenzieht oder- ausdehnt. Die Angaben eines Anéroïdes sind an und für sich ganz willkürlich und ein solches Instrument wird erst zu Höhenmessungen brauchbar, wenn es mit einem Quecksilberbarometer genau verglichen und nach jenem regulirt ist, denn erst dann lassen sich die an ihm gemachten Ablesungen auf absolutes Mass, d.h. auf die Angaben reduziren, welche man durch ein gutes Quecksilberbarometer unter gleichen Umständen erhalten haben würde. Im Folgenden wird daher stillschweigend vorausgesetzt, dass zu den Höhenmessungen Anéroïde benutzt werden, welche mit einem Normalquecksilberbarometer genau verglichen sind. Nach den Beobachtungen des berühmten französichen Physikers Eegnault, des ehemaligen Direktors der kaiserlichen Porzellanmanufactur, wiegt ein Liter atmosphärische Luft = 1,2930 Gramm und ein Liter reines Quecksilber = 13595,9 Gramm. Luft ist also 10539 mal leichter als Quecksilber, und eine Luftsäule muss daher um ebensoviel mal länger sein, als eine Quecksilbersäule, wenn sie dieser das Gleichgewicht halten soll. Lese ich also an zwei Punkten von verschiedener Höhe das Barometer ab und ist die Quecksilbersäule an dem einen 760, an dem andern 759 Millimeter lang, so muss die zwischen diesen beiden Stationen gelegene verticale Luftsäule einer Quecksilbersäule von lmm das Gleichgewicht halten, der Höhenunterschied beider Punkte daher 10,5 Meter sein. Je höher man in der Atmosphäre empor steigt, desto dünner und leichter wird die Luft, da Schwere und Druck der Atmosphäre mehr und mehr abnehmen; soll hier ebenfalls eine Luftsäule einer Quecksilbersäule von lmm das Gleichgewicht halten, so muss sie daher entsprechend länger sein und zwar in demselben Maasse, in welchem Druck und Gewicht der Luft abgenommen haben. Der Druck der Luft wird aber durch den Barometerstand selbst gemessen; bezeichnet man daher die an der untern und obern Station erhaltenen Ablesungen mit b'und b'4- b " b, so ist der mittlere Druck gleichund die Länge der Quecksilbersäule gleich bb ", die Länge der zwischen beiden Punkten gelegenen Luftsäule oder der Höhenunterschied derselben 760 H = 10,5391/g ( bb„j ( bb " ) oder V — b "
H = 16019 b'4- b "
Je wärmer die Luft ist, desto mehr dehnt sie sich aus und desto leichter wird sie. Eine Luftsäule, welche bei 0 Grad 1 Kilogramm wiegt, muss bei 273 Grad genau doppelt so lang sein, wenn sie dasselbe Gewicht 1 _ haben soll, da sie sich für jeden Grad um0,00367 ausdehnt. Das oben angegebene Gewicht von 1 Liter Luft gilt für 0 Grad; ist die Luft wärmer, so wird die Säule entsprechend länger, also H um ebensoviel grösser, so dass für die Temperatur T bb " H = 16019 b, + b„ ( 1 + 0,00367 T ) 34 wird. Setzt man noch für T, d.h. die mittlere Temperatur der Luft, das Mittel der Thermometerangaben an der untern und obern Station, so wird endlich bbtt"\ H = 16019,,, ,_„ 1 + 0,00367s
b'+b '
Hat man also an zwei Stationen gleichzeitig Barometer und Thermometer beobachtet, so lässt sich der Höhenunterschied derselben nach dieser Formel leicht berechnen, jedoch muss bemerkt werden, dass dieselbe nur angewandt werden darf bei Höhenunterschieden unter 1000 Metern, da bei ihrer Ableitung eine Voraussetzung gemacht wurde, welche bei grossen Höhenunterschieden nicht mehr hinreichend nahe erfüllt ist. Es wurde nämlich angenommen, dass der Druck der Luft proportional der Höhe abnehme, dass also in der Mitte einer Luftsäule, an deren Enden die Barometerstände b'und b " beobachtet werden, der Druck gleich
rsei. Da nun die Schwere nicht proportional der Höhe, sondern im quadratischen Verhältniss abnimmt, so ist obige Annahme nur für Höhenunterschiede bis zu 1000 Metern zulässig, für grössere bbb'Höhen hingegen statt,,.,,, zu setzen 1,1513 log. rvi wodurch die Formel übergeht in H = 18440 ( l + 0,00367log. ^ Wollte man ganz streng verfahren, so müsste man noch auf den Feuchtigkeitsgehalt der Luft und die Aenderung der Schwere mit Höhe und geographischer Breite der Stationen Rücksicht nehmen; wie wir jedoch bald sehen werden, ist dies für die praktische Anwendung nicht nothwendig.
Die Berechnung einer barometrischen Höhenmessung nach der eben mitgetheilten Formel würde etwas unbequem sein, man hat daher, um die Rechnung zu erleichtern, einen bestimmten Werth von b ', nämlich den mittleren Barometerstand im Meeresniveau ein für allemal angenommen und die Werthe von H welche verschiedenen Werthen von b " entsprechen in Tafeln zusammengestellt. Wenn z.B. an 3 Punkten beobachtet worden ist Ib'IIb "
IIIV ", so bleibt der Höhenunterschied zwischen II und III natürlich ganz derselbe, welche Werthe man auch b'beilegen mag und ebenso bleibt der Unterschied zwischen den Differenzen ( III—I ) und ( II—I ) immer der nämliche. Nimmt man z.B. b760 mm, so wird 760 il = 1Ö44U lüg- b "
III = 18440 log.
760 b ' "
und III—II = 18440 log.
V "
Setzt man also H allgemein = 18440 log.
760 und gibt b alle möglichen vorkommenden Werthe des Barometerstandes von Millimeter zu Millimeter, so entspricht jedem ein bestimmter Werth von H und die Gesammtheit bildet eine Tafel der sogenannten « rohen Seehöhen » oder « relativen Höhenzahlen ». Die letztere Bezeichnung ist jedenfalls glücklicher gewählt als die erstere, da sie schon andeutet, dass diesen Zahlen kein absoluter Werth beizulegen ist, weil im Meeresniveau nur selten der Barometerstand 760 mm vorkommen wird. Angenommen, er sei 750mm und man beobachtet ( ohne dies zu wissen ) an zwei Stationen 740 mm und 730 mm, so sind die rohen Seehöhen II = 213,4 III = 322,3 Nun liegt die erste Station keineswegs 213,4 und die zweite 322,3 Meter über dem Meere, sondern II = 107,4 III = 216,3 da die relative Höhenzahl für 750 mm = 106,0 Meter wird. Die Höhendifferenz III—II wird aber auch im ersten Falle richtig erhalten, nämlich III—II = 108,9, während die absolute Höhe um mehr als 100 Meter falsch sein würde. Die relativen Höhenzahlen dienen also nur zur Erleichterung der Kechnung. Ist die Temperatur nicht, wie in obigem Beispiele angenommen, gleich 0 Grad, so ist die gefundene Höhendifferenz
/ ttnoch mit 11 -f- 0,003671 zu multipliciren,
was leicht im Kopf geschehen kann, wenn man sich nur merkt, dass je 2,5 Grad ein Prozent Zuschlag erfordern. Die ausführlichste und bequemste Tafel der relativen Höhenzahlen ist von Max Kunze, Professor an der Forstacademie zu Tharand berechnet worden. Das barometrische Höhenmessen gestaltet sich am einfachsten, wenn man zwischen zwei gegebenen Höhen durch Interpolation eine grössere Zahl unbekannter Punkte einschaltet. Ist die Differenz der an den bekannten Stationen erhaltenen Ablesungen D, der Höhenunterschied derselben H, so ist der Werth TT eines Aneroïdtheiles -D und die Höhe der unbekannten Punkte, für welche die Differenz der Ablesung d1, d2, TTTT d3 betrug, wird h1 — d1 -^r; h2 = d2 -yr- u. s. w.
Als Beispiel mag ein kurzes Nivellement einiger durch das schweizerische Präcisionsnivellement genau bestimmter Punkte dienen, welches im Sommer 1876 mit einem Goldschmid'schen Taschenaneroïde zwischen Göschenen und Andermatt ausgeführt wurde:
( Siehe Tabelle auf der folgenden Seite. ) 15. Juni 1876.
Differenz in Höhe Zeit.
Kepère.
Aneroid.
Aneroïdth.
Metern.
barometrische.
nivellirte.
Differenz.
Meter.
10 U. M.
Bureau 669,1 1128,5 jv«:
Meter.
Meter.
Meter.
10 ü. 25 M.
6 H h 2,0 662.3 0,8 11,2 1139,7 1137,1 — 2,6 ^ 10 ü. 50 M.
a - h 1,0 664,2 4,3 60,2 1188,7 1185,5 - 3,2 if 11 ü. M.
b0,9 663,6 5,5 77,0 1205,5 1206,8 + 1,3 Ü 11 U. 20 M.
4 - 1- 1,8 661,5 7.6 106,4 1234,9 1335,3 + 0,4 11U. 55 M.
3 H r 0,8 654,1 15,0 210,0 1338,5 1339,2 + 0,7 12 ü. 10 M.
2 H h 0,7 649,7 19,4 271,6 1400,1 1402,5 + 2,4 12 U. 50 M.
Da der Höhenunterschied der beiden Endpunkte 316,9 Meter und die Differenz der an ihnen gemachten Aneroïdablesungen 22,6 Theile beträgt, so wird 1 Theil = 14,0 Meter. Multiplicirt man hiermit die Zahlen der -vierten Spalte, welche durch Subtraction aller folgenden Ablesungen von der ersten erhalten wurden, so bekommt man die Höhe der Zwischenstationen über dem Ausgangspunkte in Metern und addirt man diese Höhendifferenzen zu 1228,5, der Höhe des Anfangs-punktes, so erhält man die absoluten Höhen der Zwischenpunkte, welche mit den Zahlen der vorletzten Spalte, die das Ergebniss des Präzisionsnivellements sind, übereinstimmen sollten. Die letzte Spalte gibt die Abweichungen beider, d.h. die Fehler der mit dem Barometer bestimmten Höhen. In gleicher Weise wurden noch 5 andere Nivellements zwischen denselben Punkten ausgeführt, aus denen zusammen sich als wahrscheinlicher Fehler einer solchen Höhenbestimmung1,7 Meter ergab. Bei Höhenunterschieden bis zu 1000 Meter erhielt man aus 5 Barometernivelle-ments der Fixpunkte zwischen Airolo und dem Gotthardhospiz + 2,9 Meter. Ueber diese Grenze hinaus sollte das Interpolationsverfahren nicht ausgedehnt werden. Für approximative Bestimmungen ist es in manchen Fällen sehr angenehm, den Werth eines Aneroïdtheiles mit hinreichender Annäherung zu kennen, auch wenn keine bekannten Punkte zum Interpoliren vorhanden sind. Man kann ihn dann nach der früher mitgetheilten Formel für verschiedene Barometerstände und Lufttemperaturen berechnen, vorausgesetzt, dass eine Vergleichstabelle mit dem Quecksilberbarometer vorhanden ist. Den Goldschmid'schen Instrumenten wird daher nicht nur diese, sondern der Bequemlichkeit halber auch ein Täfelchen beigegeben, in welchem die " Werthe eines Aneroïdtheiles nach Lufttemperatur und Barometerstand geordnet zusammengestellt sind. Bei diesen einfachen Methoden, Höhenunterschiede mit nur einem Barometer zu messen, darf man nie ausser Acht lassen, dass der Barometerstand während der Zeit zwischen zwei Beobachtungen sich ändern kann und dass man um den vollen Betrag der Aenderung die zu bestimmende Höhe unrichtig erhält, wenn man diese Aenderung nicht ermitteln und in Rechnung bringen kann. Angenommen, bei unserem früheren Beispiele sei das Barometer zwischen 10 und 11 Uhr um einen Millimeter gefallen, so würde man also um 11 Uhr nicht 663,6, sondern nur 662,6 abgelesen haben; die Differenz in Aneroïdtheilen wäre dann 6,5 ( anstatt 5,5 ) und in Metern 91, also 14 Meter grösser als vorher. Sollen daher möglichst genaue Resultate erhalten werden, so muss man durch zeitweise Beobachtungen an ein und demselben Punkte die Schwankungen des Luftdrucks bestimmen und bei der Rechnung entsprechend berücksichtigen. Da jedoch bei gutem Wetter die Barometerschwankungen meist so gering sind, dass sie für manche Zwecke, namentlich bei sehr grossen Höhenunterschieden, nicht in Betracht kommen, so kann auch e i n Aneroïd zuweilen sehr angenehme Dienste leisten. Ich will nur eine Anwendung desselben hier erwähnen, die mir in den Alpen oft von wesentlichem Nutzen gewesen ist, da sie das einzige Hülfsmittel bot, mich sicher und schnell zu orientiren. Wohl keinem Alpenbesucher wird die schöne Dufourkarte unbekannt sein, wie dieselbe vom eidgenössischen Stabsbureau im Massstäbe 1: 50000 mit Höhencurven von 30 zu 30 Metern in einzelnen Blättern herausgegeben wird. Ueber den letzten Sennhütten, wo die Spuren der menschlichen Thätigkeit aufhören und oft nur noch langgestreckte Felspartieen mit einigen Wasserläufen und vielleicht noch einem Geisswege bis zum Gipfel des Berges sich hinziehen, wird es dem Auge schwer, einen Anhalt zur Orientirung und genauen Bestimmung des Punktes zu finden, wo man sich auf der Karte befindet. Die meist ganz gradlinig herabstürzenden Wasserläufe geben nur eine Richtung, hat man sich aber beim Beginn der Excursion an irgend einem bekannten Punkte der Karte die Angabe des Anéroïdes gemerkt, so lässt sich mit Hülfe des Barometers leicht die Horizontalcurve bestimmen, auf welcher man sich befindet und so durch den Schnitt beider der Standpunkt ziemlich genau ermitteln. Bekommt man auf diese Weise nur von Zeit zu Zeit einen sichern Anhaltspunkt, so findet man sich in den zwischenliegenden Partieen leicht zurecht. Das Orientiren mit Hülfe eines Barometers und der Horizontalcurven einer Karte wird jeder bald als unentbehrliches Hülfsmittel schätzen lernen, der Anwendung von ihm gemacht hat, sei es für touristische, botanische, geologische, technische, militärische und andere Zwecke. Kleine Schwankungen der Barometers sind hier ohne wesentlichen Einfluss und können daher unberücksichtigt bleiben, wie überall da, wo es sich nur um angenäherte Messungen handelt. Eine möglichst genaue Bestimmung grösserer Höhen- unterschiede verlangt zwei Beobachter und zwei Instrumente, je eines an jedem der Punkte, deren Höhenunterschied ermittelt werden soll. Die Instrumente müssen vorher genau mit einander verglichen sein, um den Einfluss der Instrumentalfehler zu entfernen und dann muss an .beiden Punkten gleichzeitig beobachtet werden. Die resultirende Druckdifferenz gibt das Gewicht der zwischen beiden Punkten befindlichen verticalen Luftsäule und die gleichzeitig beobachtete Temperatur derselben bestimmt ihre Länge. Um zu sehen, welche Genauigkeit auf diesem Wege bei grossen Höhenunterschieden erreicht werden kann und von welchen Einflüssen die Fehler hauptsächlich bedingt werden, führte ich bei Bestimmung der Richtung des Gotthardtunnels bei allen hiezu nothwendigen Bergbesteigungen ein Goldschmid'sches Aneroid der grösseren Construction mit mir. Dasselbe war in dem Theodolithenkasten gut verpackt und hat sich in Folge seiner einfachen und soliden Construction trotz aller Strapazen, denen es ausgesetzt werden musste, vortrefflich bewährt. Von Zeit zu Zeit wurde es an einer der vier meteorologischen Stationen des Gotthardgebietes mit dem Quecksilberbarometer verglichen, und es war ausgemacht worden, dass an eben diesen Stationen, in Airolo, auf dem Gotthardhospiz, in Andermatt und in Göschenen, während der Dauer der Triangulation täglich an allen geraden Tagesstunden von 6 Uhr Morgens bis 8 Uhr Abends Barometerstand und Lufttemperatur, in Airolo und Göschenen auch die Feuchtigkeit der Luft beobachet würden, während ich selbst so oft als möglich zu den gleichen Zeiten auf den einzelnen Stationen des Dreiecknetzes das Aneroïd und das Luftthermometer ablas. Da die Höhen dieser Stationen ausserdem durch ein trigonometrisches Nivellement genau bestimmt wurden, so konnte der Fehler einer barometrischen Höhenbestimmung aus je zwei correspondirenden Beobachtungen später genau ermittelt werden, da der Fehler der trigonometrisch gemessenen Höhen kaum einen Decimeter betragen kann. Aus der Berechnung von 478 im Laufe des Sommers 1874 erhaltenen correspondirenden Beobachtungen nach der früher mitgetheilten Formel ergab sich dann, dass der Fehler im Durchschnitt 7,4 Meter betrug und dass derselbe mit der Grösse des gemessenen Höhenunterschiedes bedeutend zunimmt, wie aus folgender Zusammenstellung deutlich hervorgeht:
Gemessener Höhenunterschied. Durchschnittlicher Fehler. Meter.Meter.
0— 5004,8 500 — 10006,2 1000—15009,0 1500—200011,0 Bei Anwendung der vollständigen Formel, also bei Berücksichtigung der Feuchtigkeit und des Einflusses der Schwereänderung wurden die Fehler bedeutend grösser, denn man erhielt:
Gemessener Höhenunterschied.Durchschnittlicher Fehler. Meter.Meter.
0— 5005,6 500—10009,3 1000—150016,6 1500 — 200020,4 C. Koppe.
Es erwies sich also unter diesen Umständen, d.h. bei Beobachtungen während der Monate Juli, August und September, als bei Weitem vortheilhafter, die Feuchtigkeit unberücksichtigt zu lassen und nach der einfachen Formel zu rechnen.
Den Einfluss der verschiedenen Monate und Tagesstunden zeigt die folgende Zusammenstellung.
I.
Zeit.
Juli.
August.
September 8 Uhr 6,0 10,0 10,4 10 « 6,8 8,8 10,9 12 « 6,9 6,5 11,4 1 « 4,6 7,3 7,4 2 « 3,7 6,5 8,9 4 « 4,0 6,5 6,9 6 « 5,8 5,2 — Mittel 5,4 7,3 9,6 7,4 II.
Zeit.
Juli.
August.
September.
8 Uhr + 3,0 — 7,3 — 7,4 10 « — 2,2 - 7,1 - 9,2 12 « — 4,3 — 4,8 9,5 — 3,8 - 4,8 - 4,9 2 « — 2,7 - 4,5 - 7,2 4 « - 1,8 — 3,3 - 5,1 6 « — 5,3 + 0,8 — Mittel — 2,8 4,9 - 7,7 - 5,1 In der ersten ist der durchschnittliche Fehler ohne Rücksicht auf das Vorzeichen angegeben; die zweite enthält den übrigbleibenden Fehler, wenn man die Summe der positiven und die Summe der negativen Abweichungen mit Rücksicht auf das Vorzeichen vereinigt und den Rest durch die Anzahl der Fehler dividirt. Dieser Rest würde Null sein, wenn die Summe der positiven und der negativen Fehler gleich gross wäre; ein negatives Resultat zeigt an, dass die barometrisch bestimmten Höhen zu gross sind, also eine negative Correction verlangen. Die Höhen sind also fast durchweg zu gross erhalten worden, im September aber bei Weitem mehr als im Juli und August, und auch zu den verschiedenen Tagesstunden fallen die Fehler sehr verschieden aus. Der Einfluss der Tagesund Jahreszeit auf die mit dem Barometer gemessenen Höhen geht also aus beiden Zusammenstellungen deutlich hervor.
Diese Thatsache wurde im Verlaufe des Entwicklungsganges, welchen die barometrischen Höhenmessungen durchgemacht haben, verschiedene Male beobachtet, gerieth aber eben so oft wieder in Vergessenheit, bis sie in neuerer Zeit durch Plantamour, Bauernfeind und Kühlmann genauer beobachtet und unzweifelhaft festgestellt wurde. Bauernfeind fand durch mehrtägige Beobachtungen am grossen Miesing im August 1857, dass barometrische Höhenmessungen zwischen 10 Uhr früh und 4 Uhr Nachmittags zu grosse, zu den angegebenen Zeiten aber nahe richtige Werthe liefern. Rühlmann legte seinen Rechnungen 6jährige Mittel der meteorologischen Stationen Genf und St. Bernhard zu Grunde und bestimmte aus ihnen den durch ein Nivellement festgestellten Höhenunterschied beider für alle geraden Stunden des Tages und alle Monate des Jahres. Er fand, dass die barometrisch bestimmten Höhen eine deutlich ausgesprochene tägliche und jährliche Periode zeigen, deren Verlauf mit demjenigen der Lufttemperatur nahe zusammentrifft. Das Maximum fällt auf die Mittagszeit und den Sommer, das Minimum auf die Nachtstunden und den Winter. Er erklärt diese Erscheinung dadurch, dass die Angaben der Thermometer durch Ausstrahlung des Bodens, der umstehenden Gebäude etc. in solchem Maasse beeinflusst werden, dass dieselben von der wahren Temperatur der Luft um mehrere Grade verschieden sein können. Er findet für den August als günstigste Beobachtungszeiten Morgens 7 Uhr und Abends 8 Uhr, während Bauernfeind, wie schon oben bemerkt, 10 Uhr Vormittags und 4 Uhr Nachmittags erhalten hatte. Kühlmann sucht diese Abweichung einfach dadurch zu erklären, dass er annimmt, die speciellen Verhältnisse, unter denen Bauernfeind beobachtete, seien anormale gewesen, seine Resultate hingegen, als Mittel aus langjährigen Beobachtungen, zu Regeln von allgemeiner Bedeutung mehr geeignet. Grassi, Professor der Physik in Pavia, hat desshalb ganz analoge Rechnungen für Turin und den St. Bernhard und für Aosta und den St. Bernhard ausgeführt und ebenfalls bedeutende Abweichungen von den Rühlmann'schen Daten gefunden. Die günstigsten Zeiten für barometrische Höhenmessungen werden wesentlich andere, je nach der Combination zweier Stationen, und auch aus den Beobachtungen am Gotthard geht dies deutlich hervor.
Ein noch grösserer Unterschied zeigt sich zwischen den Resultaten Rühlmann's und denen, welche Professor Weilenmann gefunden hat. In Folge starker Insolation des Bodens an klaren Sommertagen findet namentlich um die Mittagszeit und in den ersten Nachmittagsstunden ein energisches Aufsteigen der durch die Ausstrahlung des Bodens erwärmten Luft statt. Dieser aufsteigende Luftstrom reicht bis zu bedeutenden Höhen, und da die Luft direct durch die Sonnenstrahlen nur wenig erwärmt wird, so kann das Aufsteigen ohne Wärmeaufnahme oder Abgabe angenommen worden.
Die Temperaturabnahme mit der Höhe beträgt dann nur in Folge der durch die Ausdehnung der Luft beim Aufsteigen geleisteten Arbeit nahe 1° für je 100 m Höhe. Unter dieser Annahme entwickelt Weilenmann die beiden folgenden Formeln:
H = STi log.03 b.2 — hl = II worin Ti die absolute Temperatur der untern Station, gleich 273t bedeutet und bi und b2 die auf der untern und obern Station beobachteten Barometerstände sind, t ist die Angabe des hunderttheiligen Thermometers und S eine Constante, welche für die Schweiz und den Sommer durch:
log. S = 1,83200 näher bestimmt wird. Nachdem die Hülfsgrösse H berechnet, sind die beiden Correctionen:
( ' " AHAH - 2 H ( -ctt ) und + 6 H ( an dieselbe anzubringen, um den Höhenunterschied h2 — hi der beiden Stationen zu erhalten. Ebenfalls für die Schweiz und den Sommer nimmt er:
log.7,99242 — 10 und berechnet dann aus den Julimitteln um 2 Uhr Nachmittags der Jahre 1865 — 1870 ausser mehreren andern auch den Höhenunterschied der Stationen Genf und St. Bernhard, für den er die folgenden Kesultate erhält:
Höhe.
Höhe.
1866 2073,8.
1868 2072,9.
1865 2068,4.
1869 2071,7.
1867 2074,4.
1870 2077,2.
Die Monate Juni und August geben 2068,9 und 2067,4 m, also etwas zu kleine Werthe, da der wahre Höhenunterschied nach einem genauen Nivellement 2070 m beträgt. Weilemann findet also im Juli nahe richtige, im Juni und August etwas zu kleine Werthe für die gleichen Stationen und dieselbe Zeit, für welche Bühlmann gerade die grössten Fehler erhält. Wie reimt man dies alles zusammen?
Die Grundlagen barometrischer Höhenmessungen bilden wesentlich die zwei Annahmen, dass die Schichten gleichen Druckes in der Atmosphäre horizontale Flächen sind, und dass die Temperatur einer verticalen Luftsäule gleich dem arithmetischen Mittel der Thermometerangaben ist, welche an den beiden Endpunkten derselben beobachtet wurden. Abgesehen von groben Beobachtungsfehlern treten gegen Abweichungen von diesen beiden Voraussetzungen alle übrigen Fehlerquellen weit zurück. Um sich von der ersten Annahme möglichst frei zu machen, schlug Bessel vor, an mehreren Punkten von bekannter Höhenlage gleichzeitig zu beobachten und diese Stationen um das Land, in dessen Innerem eine grössere Anzahl Höhen durch das Barometer genau gemessen werden sollen, möglichst gleichmässig zu vertheilen. Er entwickelte die Rech-nungsvorschriften, um alle Beobachtungen auf den günstigsten Fall, dass dieselben für die gleiche Verticale gelten, zu reduziren, doch erst 14 Jahre später wurde das erste und einzige Mal durch Professor A. Erman in Berlin eine practische Anwendung dieser Methode gemacht und zugleich die Neigung der Schichten gleichen Druckes für den jedesmaligen Beobachtungsmoment bestimmt; So interessant und lehrreich diese Arbeit ist, so können wir doch hier nur auf dieselbe verweisen, da die tägliche Periode, welche eine so bedeutende Rolle spielt, keine Berücksichtigung fand. Um sich von dieser unabhängig zu machen, schlägt Rühlmann vor, in gleicher Weise zu verfahren, wie es Bessel angegeben, anstatt aber die Lufttemperatur durch das Thermometer zu bestimmen, dieselbe aus den beobachteten Barometerständen und den bekannten Höhenunterschieden der Stationen für möglichst viele Punkte zu berechnen und durch eine empirische Formel als abhängig von der Höhe und der geographischen Lage derselben darzustellen. Es ist nämlich klar, dass ebenso, wie sich aus den Barometerständen und Lufttemperaturen der Höhenunterschied zweier Stationen.
35 berechnen lässt, man die bekannten Höhenunterschiede benutzen kann, um aus ihnen und den Barometerbeobachtungen die Temperatur zu berechnen, welche die zwischen zwei Stationen gelegene Luftsäule zu einer bestimmten Zeit gehabt haben muss, und es leuchtet sofort ein, dass man auf diese Weise von den Fehlern der Thermometerangaben ganz unabhängig wird und zuverlässige Resultate erhalten muss, wenn es gelingt, den Verlauf der wahren Temperatur der Luft für das ganze Gebiet der Messung durch die abgeleitete Formel richtig darzustellen. Wieviel Stationen hierzu nothwendig sind, wie eng sie über das Vermessungsgebiet vertheilt sein, und welche Höhenunterschiede unter ihnen stattfinden müssen, um sichere Resultate zu erhalten, kann nur durch practische Versuche ermittelt werden. Diese aber fehlen bis jetzt gänzlich. Rühlmann selbst äussert sich darüber folgendermassen: « Leider sind mir nicht Beobachtungsresultate eines Systèmes meteorologischer Stationen zugänglich gewesen, welche den Bedingungen der Methode genügt hätten, so dass es leider unmöglich war, ein Zahlenbeispiel beizufügen. » Es ist jedenfalls kein gutes Zeichen für die practische Verwendbarkeit einer Methode, wenn ein Beobachtungsmaterial von einigen hundert Jahren nicht genügt, ein Zahlenbeispiel zu liefern. Die Beobachtungen im Gotthardgebiet sind unter so günstigen Verhältnissen angestellt worden, alle Punkte liegen so nahe zusammen, und die vier meteorologischen Stationen haben solch'verschiedene Höhen, dass es gerechtfertigt schien, an ihnen die Methode zu versuchen. Die Resultate haben den Erwartungen nicht entsprochen; die Abweichungen der berechneten Höhen von den wahren werden sehr bedeutend, ein Beweis, dass auch hier die vorhandenen Hülfsmittel nicht genügt haben, den Verlauf der Lufttemperatur richtig darzustellen, und so wird die Kühlmann'sche Methode, so rationell dieselbe erscheint, in practischer Beziehung auf sehr ausnahmsweise, mehr ideale Fälle beschränkt bleiben. Es muss also ein anderer Weg gesucht werden, genauere Resultate zu erhalten. Doch kehren wir zunächst zu dem Versuche zurück, die im Vorigen mitgetheilten Widersprüche zwischen den Ergebnissen verschiedener Beobachtungen zu erklären. Wie wir bereits gesehen haben, gibt die Weilenmann'sche Formel für Sommer-Mittage günstige Resultate unter Anwendung bloss der Temperatur der untern Station; der Gedanke lag nahe, dasselbe mit der an der oberen Station beobachteten Temperatur zu versuchen. Alle so erhaltenen Höhenunterschiede fallen bedeutend zu gross aus, und dies kann darin seinen Grund haben, dass die Thermometerangaben nicht in allen Höhen um gleich viel von der wahren Temperatur der Luft abweichen. Benutzt man von den am Gotthard gemachten Beobachtungen die Tage, an welchen auf allen fünf Stationen zu gleicher Zeit beobachtet wurde, berechnet aus den bekannten Höhenunterschieden und beobachteten Barometerständen je zweier Stationen die wahre Temperatur der dazwischen gelegenen Luftsäule und vergleicht diese mit den Angaben der Thermometer, so sieht man deutlich, dass die Differenz zwischen den beobachteten und den be- rechneten Temperaturen wesentlich von der verschiedenen Höhe der Stationen abhängt. Bis zu 1800 m ist die wahre Temperatur stets kleiner als das Mittel der Thermometerangaben, für etwa 1500 m werden beide gleich und für kleinere Höhen überwiegt die berechnete Temperatur.
Um diese Erscheinung für die verschiedenen Tagesund Jahreszeiten genauer verfolgen zu können, wurde das System meteorologischer Stationen der Süd-, Ost-und Central-Schweiz gewählt, da diese ihres verhältnissmässig geringen horizontalen, aber sehr bedeutenden verticalen Abstandes halber für solche Untersuchungen am besten geeignet zu sein schienen. Für die zwölf Stationen:
Höhe.Höhe.
Julier 2244 MeterKlosters1207 Meter Gotthard 2100 « Thusis711 « Bernhardin 2070 « Castasegna 700 « Sils1810 « Chur603 « Bevers 1715 « Lugano275 « Platta 1379 « St. Vittore 268 « wurden die dreimaligen täglichen Barometer- und Temperaturbeobachtungen der Jahre 1868—1873 zu monatlichen Mitteln vereinigt, dann 29 verschiedene Combinationen der Beobachtungsstationen gebildet und aus den 6jährigen Mitteln der Barometerstände und den bekannten Höhenunterschieden der Stationen die jedes-malige wahre mittlere Lufttemperatur der zwischenliegenden Luftsäule berechnet. Da die Genauigkeit der so berechneten Temperaturen unter sonst gleichen Verhältnissen um so geringer ausfällt, je kleiner der Höhenunterschied der betreffenden zwei Stationen ist, so wurde sie diesem Höhenunterschiede direct proportional gesetzt und aus den 29 Combinationen dementsprechend Mittelwerthe gebildet. Um auch noch den Feuchtigkeitsgehalt der Luft nicht unberücksichtigt zu lassen, wurde für jeden Monat ein mittlerer Werth desselben nach den in den schweizerischen meteorologischen Beobachtungen vom Professor Weilenmann gegebenen Zusammenstellungen angenommen. Von den durch diese langwierige Rechnung erhaltenen Resultaten genügt es, die Zahlen für Januar und August hier anzugeben, da der kälteste und wärmste Monat im Gebirge den Verlauf während des ganzen Jahres hinreichend anschaulich machen.
J an u a r.
Meerealiöhe.
Berechnete Temperaturen.
Meter.
7 Uhr.
1 Uhr. 9 Uhi Grad.
Grad.
Grad.
1850 — 8,9 - 7,9 - 8,6 1690 — 4,5OK 4,2 1475 - 1,6 - 1,9 - 2,3 1390 - 1,0 — 0,6 — 1,0 1250
+ 0,1 + 0,2 1120 + 0,1 + 0,6 + 0,1 1035 + 1,7 + 2,4 + 2,5 480 + 2,3 + 4,3 + 4,3 660C. Koppe.
August.
Meereshöhe.
Berechnete Temperaturen.
Meter.
7 Uhr.
1 Uhr.
9 Uhr.
Grad.
Grad.
Grad.
1850 + 4,6
+ 7,0
+ 4,0 1690 + 9,7 + 12,3 + 10,1 1475 + 12,2 + 13,9 + 12,2 1390 + 13,3 + 15,1 + 14,7 1250 + 14,4 + 15,7 + 15,1 1180 + 14,0 + 16,8 + 16,9 1035 + 16,8 + 18,5 + 18,6 480 + 20,3 + 23,0 + 24,3 Die beobachteten Temperaturen sind hingegen:
J a n u a r.
Meereshöhe.
Beobachtete Temperaturen.
Meter.
7 Uhr.
1 Uhr.
9 Uhr.
Grad.
Grad.
Grad.
2244 — 9,9 - 6,7 — 9,9 2100 - 9,1 — 9,0 2070 - 8,4 Fi fi 0,0 — 8,3 1810 - 11,4 - 4,2 - 9,8 1715 - 14,2 - 5,7 — 11,5 1379 - 5,4 - 3,8 - 4,5 1207 — 6,3 - 1,2 - 5,4 711 — 3,6 + 0,8 - 2,1 700 — 1,0 + 1,4 — 0,6 603 - 2,4 + 1,3 - 1,1 275 — 1)0 + 4,0 — 0,9 268 - 1,5 + 4,5 - 0,4 Au gust.
Meereshöhe.
Beobachtete Temperaturen.
Meter.
7 Uhr.
1 Uhr.
9 Uhr.
Grad.
Grad.
Grad.
2244 + 5,9 + 10,8 + 6,2 2100 + 6,3 + 10,2 + 6,7 2070 + 8,1 + 12,0 + 7,7 1810 + 7,9 + 15,0 + 8,9 1715 + 7,1 + 16,4 + 9,7 1379 + 10,0 + 17,4 + 11,2 1207 + 11,5 + 16,9 + 11,5 711 + 14,6 + 21,4 + 15,9 700 + 16,2 + 21,3 + 17,0 603 + 14,2 + 20,8 + 16,1 275 + 18,1 + 25,2 + 19,2 268 + 17,6 + 24,2 + 18,9 Die Eesultate, welche sich aus d«r Vergleichung der eben mitgetheilten berechneten und beobachteten Temperaturen ergeben, sind sehr auffallender Natur und werden am besten anschaulich gemacht, wenn man die Temperaturen als Ordinaten und die Meereshöhen, für welche sie gelten, als zugehörige Abscissen aufträgt und berechnete sowohl wie beobachtete Temperaturen durch eine continuirliche Linie verbindet.
Dasjenige, was durch die Beobachtungen am Gotthard nur angedeutet war, tritt hier nun in überraschen^ der Weise zu Tage, indem für keine Tages- und keine Jahreszeit in verschiedenen Höhen die Differenz zwischen beobachteter und berechneter Temperatur dieselbe bleibt. Morgens und Abends ist für alle Monate des Jahres für Stationen, welche nur einige hundert Meter über dem Meere liegen, die beobachtete Temperatur erheblich niedriger als die berechnete, für Stationen hingegen, die über 2000 Meter liegen, ist dieselbe für alle Tages- und Jahreszeiten bedeutend höher als die berechnete Temperatur. Der Schnitt beider Curven, d.h. die Stelle, wo Beobachtung und Rechnung dasselbe geben, fällt je nach der Tageszeit auf verschiedene Höhen und zwar so, dass er Morgens und Abends auf grosse, Mittags hingegen auf geringe Höhen zu liegen kommt. Von Morgens bis Mittags und wieder umgekehrt von Mittags bis Abends durchläuft er also alle Zwischenstufen und es ist nun unmittelbar anschaulich, wie man als günstigste Zeiten für die Beobachtung der Lufttemperatur ganz verschiedene Resultate erhält, je nach der grössern oder geringern Meereshöhe der Stationen, aus denen man diese Zeiten ableitet. Man braucht daher nicht mehr mit Rühlmann die atmosphärischen Zustände, unter denen Bauernfeind am grossen Miesing beobachtete, als anormale anzusehen, weil sie als günstigste Zeiten zur Bestimmung der Lufttemperatur 10 Uhr und 4 Uhr zum Resultate hatten, während die Combination Genf-St. Bernhard ganz andere ergab. Die letzteren haben so wenig allgemeine Gültigkeit als die ersteren, und ganz dasselbe gilt von den Zeiten, die Grassi durch Turin-St. Bernhard und Aosta-St. Bernhard fand, und denen, die der Gotthard ergab. Alle sind nur spezielle Fälle eines .allgemeineren Gesetzes. Auch der Widerspruch zwischen den Rechnungen Rühlmanns und denen Weilenmanns, indem ersterer für die Mittagsstunden und den Juli die grössten Abweichungen der baro- metrisch bestimmten Höhe Genf-St. Bernhard fand, letzterer zur ganz gleichen Zeit dieselbe Höhe mit der Temperatur der untern Station richtig erhielt, erklärt sich jetzt sehr einfach dadurch, dass für den Mittag der Sommermonate die Differenz zwischen beobachteter und berechneter Temperatur ` für kleine Höhen ( Genf ) gleich Null, für grosse Höhen ( St. Bernhard ) sehr bedeutend wird. Weilenmann nimmt nur die Temperatur der untern Station, und da diese richtig ist, so erhält er auch richtige Resultate; Rühlmann nimmt das Mittel aus den Temperaturen der obern und untern Station und erhält, da dieses die wahre Temperatur bei Weitem überwiegt, auch eine zu grosse barometrische Höhe. Aus obiger Vergleichung folgt weiter das wichtige Resultat, dass die Lufttemperatur im Allgemeinen nicht in gleichem Masse wie die Höhe abnimmt, sondern in den unteren Luftschichten langsamer, in den oberen bedeutend rascher als jene. Eine der wesentlichsten Grundbedingungen, auf welcher die barometrische Höhenberechnung nach der früher mitgetheilten Formel beruht, ist aber dann nicht mehr erfüllt, denn die mittlere Temperatur einer Luftsäule ist in diesem Falle nicht mehr gleich dem Mittel der Thermometerangaben, welche an ihren Enden beobachtet wurden, auch wenn die Thermometer die richtige Temperatur der Luft anzeigen. Aus beiden Gründen, einmal weil die wahre Lufttemperatur im Allgemeinen nicht mit den Thermometerangaben übereinstimmt und dann, weil die Temperatur der Luft nicht proportional der Höhe abnimmt, muss man unrichtige Resultate erhalten, wenn man das Mittel der Thermometerablesungen als mittlere Luft- temperato in Rechnung bringt und dies um so mehr, je grösser der Höhenunterschied ist, welcher gemessen werden soll. Daher fallen auch die früher mitgetheilten Correctionen der barometrisch bestimmten Höhen überwiegend negativ aus und nehmen mit der Grösse des gemessenen Höhenunterschiedes bedeutend zu. Es fragt sich nun, ist es nicht möglich, Resultate aus den Beobachtungen zu ziehen, welche der Wahrheit näher kommen? Die Rühlmann'sche Methode hat, wie schon erwähnt, keine günstigen Resultate ergeben, zunächst versuchten wir es daher mit der ebenfalls bereits mitgetheilten Weilenmann'schen Formel. Hier waren die Abweichungen schon geringer, am Genauesten aber stimmten die berechneten Höhen mit den wahren überein, wenn man die Grundlagen, auf denen die Weilenmann'sche Formel beruht, etwas weiter verfolgt und darnach das Verfahren modificirt.
Wie aus der Vergleichung der beobachteten und berechneten Temperaturen hervorgeht, stimmen beide an Sommermittagen in nicht sehr bedeutenden Höhen so nahe überein, dass man durch Thermometerbeobachtungen um diese Zeit dort jedenfalls nahe richtige Resultate für die Lufttemperatur erwarten darf. Um dieselbe Zeit geschieht auch die Abnahme der Temperatur mit der Höhe am nächsten dieser proportional. Berücksichtigt man weiter, dass der Vergleichung Mittelwerthe zu Grunde liegen, in welchen gute wie schlechte Beobachtungstage enthalten sind, so steht zu erwarten, dass wenn man nur die ruhigen und klaren Sommertage auswählt, beide Erscheinungen mit weit grösserer Regelmässigkeit stattfinden werden. Beobachtet man also unter solchen Verhältnissen an zwei bekannten Stationen, von denen z.B. die eine auf 1000, die andere auf 2000 Meter Höhe liegt, so wird man die Lufttemperatur der untern Station nahe richtig erhalten und die gleiche Temperaturabnahme, welche die Barometerbeobachtung an der obern Station ergibt, ohne erheblichen Fehler noch mehrere 100 oder 1000 Meter sich fortgesetzt denken und eine dort gelegene unbekannte Station hiernach bestimmen können. Für die praktische Anwendung würde es unbequem sein, jedesmal aus den Beobachtungen an den beiden bekannten Stationen die Temperaturabnahme mit der Höhe ableiten zu müssen, einfacher ist es, eine bestimmte Abnahme der Temperatur mit der Höhe von vornherein anzunehmen; kommt diese der Wahrheit hinreichend nahe, so kann man dann den Fehler, der sich bei der Berechnung der bekannten Höhe ergibt, proportional der Höhe an die unbekannte anbringen. Für den vorliegenden Fall genügt z.B. die Annahme, dass an Sommermittagen das Aufsteigen der Luft ohne Aufnahme und Abgabe von Wärme und die Abkühlung nur in Folge der Ausdehnung stattfinde, also eine Berechnung nach der schon früher mitgetheilten Weilenmann'schen Formel.
Zum Beispiel wurden am 25. September an den 3 Stationen Airolo, St. Gotthard und Fibbia die folgenden Beobachtungen gemacht: 25. Sept. Airolo.Gotthard.Fibbia.
1 Uhr 670,0 20,6 600,8 10,9 558,8 8,0 2 Uhr 669,8 19,7 600,8 10,0 558,7 9,0 Mittel 669,9 20,15 600,8 10,45 558,75 8,5 Die Weilenmann'sche Formel H = S Ti log. ~ gibt mit Ti = 273 -j- 20,15 = 293,15 und log. S = 1,23200 zunächst Hi = Airolo-Gotthard = 941,4 H2 = Airolo-Fibbia = 1568,8 mit log. " 7T = 7,99243 — 10 werden die Correctionen / A Hi1/2 Hl ( -ött14'85
+ 1/o Hl ( w16
-tt41'25
+ Ve H20,72
also
Airolo-Gotthard = 941,4 — 14,85 -f 0,16 = 926,7 Airolo-Fibbia = 1568,8 — 41,25 -j- 0,72 = 1528,3 Da der wahre Höhenunterschied Airolo-Gotthard = 922,4 Meter ist, ergibt die Eechnung 4,3 Meter zu viel, man wird also den Höhenunterschied Airolo-Fibbia um 1528 X 4,3 = 7,1 Meter verkleinern müssen. Dann wird Airolo-Fibbia = 1521,2 Meter. Nach der trigonometrischen Messung beträgt er 1522,8, also nur 1 bis 2 Meter mehr, wovon noch die halbe Signalhöhe in Abzug gebracht werden könnte, da ich am untern Signalrande sitzend beobachtete.
Der wahrscheinliche Fehler aus 40 im Laufe des Sommers angestellten derartigen Höhenmessungen wird ± 1,90 Meter.
Dies ist, glaube ich, Alles, was man von einer einmaligen barometrischen Höhenmessung im Hochgebirge verlangen kann und zugleich der beste Beweis, dass mit guten und genau verglichenen Aneroïden bei Beachtung der nöthigen Vorsichtsmassregeln auch bei grossen Höhenunterschieden sehr brauchbare Resultate erhalten werden können. Nimmt man anstatt der Mittagsbeobachtungen die des ganzen Tages von Morgens 10 bis Abends 4 Uhr, so wird der wahrscheinliche Fehler einer Höhenbestimmung = 2,09 Meter, also trotz der grösseren Anzahl der Beobachtungen etwas grösser, ein Beweis, dass die der Berechnung zu Grunde gelegten Annahmen um die Mittagszeit am nächsten erfüllt sind. Immerhin ist der wahrscheinliche Fehler auch dann noch so gering, dass man obiges Verfahren auch in den der Mittagszeit nahe gelegenen Vormittags- und Nachmittagsstunden noch mit Vortheil wird anwenden können. Nach den im Vorigen mitgetheilten Resultaten wird man zu der Annahme genöthigt, dass das Mittel der an zwei Stationen abgelesenen Thermometerangaben von der wahren Temperatur der zwischen beiden gelegenen Luftsäule sehr verschieden sein kann, und es fragt sich nun, worin hat diese Abweichung ihren Grund. Es sind hier zwei wesentlich verschiedene Fälle möglich, welche beide zu demselben Resultate führen s.'müssten, denn einmal kann die in der Nähe des Bodens befindliche Luftschicht durch die unmittelbare Berührung mit ihm eine andere Temperatur annehmen als die entfernteren Luftschichten, und andererseits kann ein Thermometer in- Folge der Beeinflussung durch Ausstrahlung der umliegenden Gegenstände ganz etwas Anderes angeben, als die wahre Temperatur der Luft, in welcher es sich befindet. Manchem Alpenbesucher wird es beim Bergsteigen schon vorgekommen sein, dass er abwechselnd in Schichten von sehr verschiedener Temperatur gelangte, ohne dass sich eine besondere Luftströmung in Folge der ungleichen Erwärmung geltend machte. Namentlich bei ruhigem Wetter könnte somit die Temperaturabnahme mit der Höhe in der Nähe des Bodens eine ganz andere sein als weiter oben, und wenn dann das Thermometer auch die wahre Temperatur der Luft in seiner unmittelbaren Umgebung anzeigte, so könnte das Mittel der an zwei Stationen erhaltenen Thermometerablesungen doch wesentlich verschieden sein von der wahren mittleren Temperatur der ganzen Luftsäule. Diese letztere Temperatur bedingt aber die Länge dieser Luftsäule, deren Gewicht durch die Barometerablesungen bekannt ist. Bei den bis jetzt in verschiedener Höhe über dem Boden gemachten Thermometerbeobachtungen waren die absoluten Höhenunterschiede zu gering, um sichere Schlüsse in dieser Hinsicht aus ihnen ziehen zu können. Der andere Fall, dass das Thermometer etwas anderes angibt, als die Temperatur der es umgebenden Luft, ist ebensowohl möglich, denn ein Thermometer zeigt in der Nähe des Ofens etwas anderes, .'HI jenachdem sich ein Schirm zwischen ihm und dem Ofen befindet, während die Temperatur der Luft offenbar in beiden Fällen die gleiche ist. Wie lässt sich nun entscheiden, welcher von beiden Fällen in der Natur stattfindet? Die aus Baromoterbeobachtungen rückwärts berechneten Temperaturen gelten nur für das Mittel der ganzen Luftsäule und können für das, was an einer einzelnen Station stattfindet, keinen Anhalt liefern, unmittelbare Thermometerbeobachtungen in verschiedenen Höhen würden sehr umständlich sein, da für einigermassen zuverlässige Resultate grosse Höhenunterschiede erforderlich sind und es doch immer, um das Thermometer aufzuhängen, eines Gerüstes etc. bedürfte, dessen Ausstrahlung wieder störend wirken müsste. Ich glaube, der einfachste und bequemste Weg, zu einem Resultate zu gelangen, dürfte der folgende sein, auf den ich die Besucher der Hochalpen besonders aufmerksam machen möchte, da bei jeder Bergbesteigung werthvolle Beobachtungen leicht gemacht werden können, die im Jahrbuche gesammelt für die Meteorologie von wesentlichem Nutzen sein würden. Wie allgemein bekannt, enthält die Luft stets eine grössere Menge Wasser in unsichtbarer Form als Wasserdampf aufgelöst, welcher bei Abkühlung der Luft über ihren Sättigungspunkt als Nebel, Regen oder Schnee ausgeschieden wird. Die Fähigkeit der Luft, Wasserdampf aufzunehmen, hängt ab von ihrer Temperatur; je wärmer es ist, desto mehr Wasser kann im Allgemeinen verdunsten und desto mehr ist erforderlich, bis ein Raum von bestimmter Grösse gesättigt ist Nach den Versuchen von Magnus und Regnault genügen z.B. bei Null Grad 4,9 Gramm per Cubicmeter, während bei 10 Grad 9,4 Gramm, bei 20 Grad 17,2 Gramm u. s. w für dieselbe Raumes-einheit erforderlich sind, bis die Luft vollständig gesättigt ist. Besitzt man also ein Mittel, die Menge Wasserdampf genau zu messen, weiche nothwendig ist, die Luft gerade zu sättigen, so kann man umgekehrt aus der Menge des erforderlichen Wassers einen Rückschluss machen auf die Temperatur der Luft, welche dann offenbar die wahre Temperatur derselben sein muss, und vergleicht man diese mit der Thermometer-ablesung, so sieht man, ob das Thermometer die wahre Temperatur der Luft angibt oder nicht.
Die Methoden, den Feuchtigkeitsgehalt der Luft zu bestimmen, sind mannigfacher Art. Entweder misst man unmittelbar das Gewicht des Dampfes, welcher in einem Räume von bestimmter Grösse, z.B. einem Cubicmeter enthalten ist, oder man bestimmt die Temperatur, bei welcher der Raum gesättigt sein würde, und entnimmt der erwähnten, von Regnault aufgestellten Tabelle die dieser Temperatur entsprechende Spannkraft des Dampfes, oder man schliesst aus der Energie der Verdunstung und der durch dieselbe bewirkten Abkühlung eines benetzten Thermometers auf den Sättigungsgrad der Luft, oder endlich man beobachtet das Verhalten gewisser organischer Substanzen, welche die Eigenschaft haben, je nach dem Prozent-gehalte der Luft an Wasserdampf mehr oder weniger Feuchtigkeit in sich aufzunehmen und hiebei ihre Gestalt entsprechend zu verändern. Die erste und letzte Methode sind von der durch das Thermometer ge- tnessenen Temperatur unabhängig, während bei der zweiten und dritten gerade die Angabe des Thermometers massgebend ist. Man kann die erwähnten Messungen daher auch in der Weise anstellen, dass man den Feuchtigkeitsgehalt der Luft einmal mit Hülfe des Thermometers bestimmt und dann dieselbe Messung nach einer andern Methode vornimmt, bei welcher kein Thermometer gebraucht wird.
Ergeben beide Methoden dasselbe Resultat, so gibt das Thermometer offenbar die wahre Temperatur der Luft, sind die Resultate hingegen verschieden, so ist dies nicht der Fall. Am einfachsten und bequemsten kann eine solche Vergleichung nach der dritten und vierten Methode vorgenommen werden, d.h. indem man zu gleicher Zeit ein Psychrometer und ein Haarhygrometer beobachtet.
Ich hatte schon vor einigen Jahren, als ich zur Bestimmung der Richtung des Gotthardtunnels fast täglich Bergbesteigungen machen musste, die Absicht, eine längere Vergleichsreihe beider Instrumente zugleich mit den übrigen Beobachtungen vorzunehmen, bin aber damals zu keinem Resultate gelangt, da die Haarhygrometer zu unvollkommen waren. Jeder Transport brachte Aenderuugen derselben hervor, die ich erst erkennen konnte, wenn ich wieder unten war, und dann liess sich nicht mehr entscheiden, wann die Aenderungen eingetreten waren, ob vor oder nach der Besteigung. Ich sah bald, dass ich auf diese Weise zu keinem Resultate gelangen konnte, möchte mir aber jetzt erlauben, Andere auf diese interessanten Beobachtungen aufmerksam zu machen und zugleich eine Ein- 36 562a Koppe.
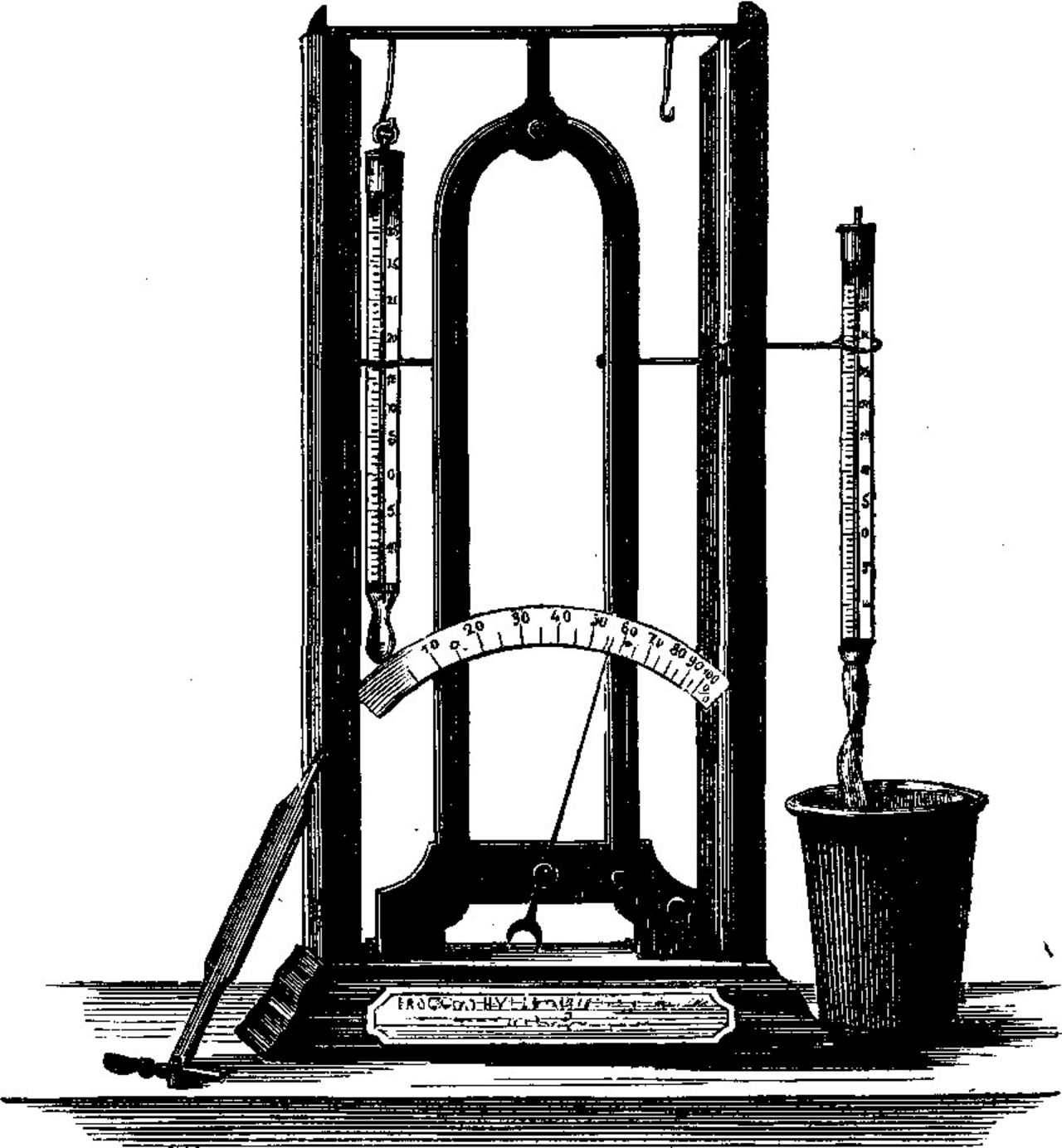
richtung des Instrumentes zu beschreiben, welche die oben erwähnten Mängel beseitigt und genaue Bestimmungen zulässt. Durch die Versuche von Saussure und später diejenigen von Gay-Lussac und Regnault ist hinreichend dargethan, dass ein Haar, auf angemessene Weise vom Fett befreit, dem Grade der relativen Feuchtigkeit des Raumes, in welchem es sich befindet, mit grosser Regelmässigkeit folgt, so dass man dasselbe als Hygrometer benutzen kann. Regnault überzeugte sich durch Versuche, dass gut construirte Haarhygrometer die relative Feuchtigkeit bis auf einzelne Prozente genau anzugeben im Stande sind; nichtsdestoweniger glaubte er vom Gebrauche dieser Art Hygrometer abrathen zu müssen, da die von ihm benutzten Instrumente zu leicht in Unordnung geriethen, um, wenn ein Transport derselben nothwendig war, auch nur einigermassen zuverlässige Resultate erwarten zu lassen. Dies gilt auch jetzt noch von allen den Haar-hygrometern gegebenen Formen, sowie von allen Feuchtigkeitsmessern, welche auf den hygroscopischen Eigenschaften organischer Substanzen beruhen, unter denen das Haarhygrometer unstreitig am regelmässigsten functionirt. Die Störungen, welche diese Instrumente'.,durch den Transport etc. erleiden, fallen theilweise dem Mechanismus zur Last, welcher die durch denWechsel der Feuchtigkeit bedingte kleine Verlängerung oder Verkürzung des Haares zur Anschauung bringen soll, theilweise haben sie ihren Grund in einer wirklichen Veränderung, d.h. einer von dem Feuchtigkeitsgrade unabhängigen Aenderung der Länge des Haares. Ein gereinigtes Menschenhaar hat im Mittel Ueber barometrisches Hohenmessen.
eine Tragkraft von 100 Gramm und eine Elastizität von 33 Prozent, d.h. es lässt sich um Va seiner Länge auseinanderziehen, ehe es zerreisst. Ist es im Hygrometer um eine Axe geschlungen, welche 4 mm Durchmesser hat, nimmt ferner die Scale einen Quadranten ein und denkt man sich dieselbe in 100 gleiche Theile getheilt, so entspricht ein solcher Theil einer Veränderung der Länge des Haares von wenigen Hundert-steln eines Millimeters, und wenn das Haar selbst einige hundert Millimeter lang ist, so lässt sich schon a priori schliessen, dass auch eine wirkliche Dehnung des Haares, welche eine Verstellung des Zeigers um mehrere Prozente bewirkt, im Vergleich zur ganzen Länge des Haares so gering ist, dass sie keine wesentliche Veränderung der hygroscopischen Eigenschaften des Haares veranlasst, sondern nur den Nullpunkt der Scale verschiebt. Dies gilt selbstredend von allen den Verstellungen, welche im Mechanismus ihren Grund haben, so dass, wenn man für ein Haar die Prozentscale einmal genau bestimmt hat und das Hygrometer in Folge des Transportes und Gebrauches ganz unrichtig zeigt, man doch eine ganz identische Prozentscale erhält, wenn man dieselbe durch neue Vergleichungen noch einmal bestimmt. Ein solches Hygrometer wird daher wieder ganz richtig functioniren, wenn man die Mittel besitzt, einen Punkt der Scale zu controliren und zu berichtigen, was durch zahlreiche practische Versuche hinreichend bestätigt worden ist. Das ganze Hygrometer ist daher in ein Blechkästchen gestellt, welches vorn durch eine Glasscheibe und hinten durch einen Schieber geschlossen werden kann; vor letzterem ist ein mit dünnem Zeuge über-spanntes Rähmchen in einer Nuth eingeschoben. Soll das Instrument zu Beobachtungen benutzt werden, so wird die auf das Rähmchen aufgezogene Membrane mit Wasser gut angefeuchtet und eingeschoben. Das Kästchen füllt sich dann in kurzer Zeit vollständig mit Feuchtigkeit, da die verdunstende Oberfläche verhältnissmässig sehr gross ist; und da sich das Haar seiner ganzen Länge nach in unmittelbarer Nähe der nassen Membrane befindet, so wird sich dasselbe rasch mit Feuchtigkeit sättigen und der Zeiger bis zu einem Punkte vorrücken, welcher dieser vollkommenen Sättigung entspricht, und dort stehen bleiben. Dieser Punkt sollte der Theilstrich für 100 °/o sein, in Folge der Veränderungen des Instrumentes beim Transport etc. wird er es in vielen Fällen nicht sein. Man hat dann nur einen Uhrschlüssel durch das oben in der Glasscheibe befindliche Loch auf die Axe aufzusetzen, in welcher das obere Ende des Haares befestigt ist und durch Drehen den Zeiger auf 100 zu führen. Um die Reibung der Axe leichter zu überwinden, ist es gut, etwas auf den Fuss des Hygrometers zu klopfen und neu einzustellen, wenn durch das Klopfen eine kleine Verrückung des Zeigers hervorgebracht wird. Dann ist das Instrument justirt und wird, nachdem man Schieber, Membrane und Glas entfernt hat, einige Minuten später den Feuchtigkeitsgrad der Luft richtig anzeigen. Ein Psychrometer lässt sich mit der beschriebenen Einrichtung bequem verbinden, wie es in der Figur angedeutet ist. Das trockne Thermometer bleibt im Blechkästchen, das zu befeuchtende wird herausgenommen und aussen in den an der Seite angebrachten Halter gesteckt, so dass das verdunstende Wasser das Haarhygrometer nicht beeinflussen kann Der ganze Apparat ist in ein kleines Etui verpackt und kann so bequem überall mit hingenommen werden* ). Ausser für den erwähnten Zweck werden solche Feuchtigkeitsmessungen in grösseren Höhen für die ganze Meteorologie von Wichtigkeit sein, da über den Gehalt der Luft an Wasserdampf, welcher bei allen Vorgängen in der Atmosphäre eine so wichtige Rolle spielt, noch sehr wenig genaue Bestimmungen vorhanden sind. Das Ziel der Meteorologie ist das Auffinden allgemeiner Gesetze, welche die Vorgänge in der Atmosphäre bedingen; wären dieselben bekannt, so liesse sich die Witterung eines bestimmten Tages ebenso genau voraussagen, wie das Eintreten einer Verfinsterung des Mondes oder der Sonne. « Gäbe es einen Verstand », sagt Laplace, « der alle Kräfte kennt, welche in einem gewissen Zeitpunkte die Natur beleben, sowie alle gegenseitigen Beziehungen der Wesen in ihr, und wäre derselbe fähig, diese gegebenen Grossen in Rechnung zu stellen, so würde er die Bewegung der Himmelskörper, wie die der leichtesten Staub-flöckchen, in demselben analytischen Ausdrucke umfassen. Für ihn wäre nichts ungewiss; Vergangenheit und Zukunft ständen klar vor seinen Augen. In der Entwicklung der Astronomie hat der menschliche Geist sich zu einem schwachen Abbilde dieses Verstandes erhoben. » Anmerkung. Laplace. Essais philosophiques sur les probabilités: Une intelligence, qui pour un instant donné, connaîtrait toutes les forces,dont la nature est animée et la situation respective des êtres, qui la composent, si d' ailleurs elle était assez vaste pour soumettre ces données à l' analyse, embrasserait dans la même formule les mouvements des plus grands corps de l' univers et ceux du plus léger atome; rien ne serait incertain pour elle, et l' avenir comme le passé serait présent à ses yeux. L' esprit humain offre dans la perfection, qu' il a su donner à l' astronomie une faible esquisse de cette intelligence.
V
IV.
Kleinere Mittheilungen.