Die Erdkrümmung

VON GEORG SCHMIDT, ZÜRICH

Unter diesem sehr allgemeinen Titel möchte ich einige Angaben wiedergeben über eine Erfahrung, die man beim Betrachten von Bergpanoramen immer wieder macht, dass nämlich hohe, aber weit entfernte Berge fast unkenntlich werden, indem sie im Vergleich mit näheren viel zu niedrig erscheinen oder dass man sie überhaupt nicht mehr sieht. Dieses Phänomen hängt natürlich zusammen mit der Kugelgestalt unserer Erde.

Der Artikel bezweckt keineswegs, ungewohnte Leser mit mathematischen Formeln zu plagen, sondern einen allgemeinen Begriff über die Grössenordnung dieser Werte zu vermitteln. Ich beschränke mich daher in mathematischer Beziehung auf ein Minimum, das mir aber für das Verständnis der Beispiele doch nötig erscheint.

Zuerst einige Definitionen:

Der scheinbare Horizont ist die Linie, welche eine horizontale Ebene, die durch das Auge des Beobachters geht, an Himmel oder Berghängen ausschneidet. Stehen wir auf einem hohen Berge, so kann diese rundherum horizontale Linie ganz in der Luft sich befinden ( Fig. 1 ).

Der natürliche Horizont ist die Berührungslinie einer Kegelfläche mit der Erde, deren Spitze im Auge des Beobachters liegt und deren Mantellinien die Erde tangieren. Dieser sehr flache Kegel wird nur auf dem Meer zu einem Kreiskegel; seine Berührungslinie mit dem Wasser heisst die Kimm. Für das Auge des Schwimmers werden scheinbarer Horizont und natürlicher Horizont identisch.

Der wahre Horizont ist ein Begriff der Astronomen und bedeutet die Parallelebene zum scheinbaren Horizont durch den Erdmittelpunkt.

Der Beobachtungs-Geländewinkel, meist nur Geländewinkel genannt, ist der Winkel zwischen Sehstrahl S und dem scheinbaren Horizont. Er kann positiv oder negativ sein, je nachdem das anvisierte Objekt höher oder niedriger ist als der Beobachter. Er wird zweckmässig angegeben in RadiuspromillenOo)- Man könnte natürlich ebensogut in Gradenmessen; allein dieses Mass ist für uns unbequem gross und lässt sich nicht so leicht errechnen.

1 Radiuspromille ist der Winkel, unter dem 1 m aus der Distanz von 1 km = 1000 m gesehen wird.

Fig. 2 ( nicht maßstäblich ) Das Radiuspromille ist zugleich ein sehr praktisches Mass: bei ausgestrecktem Arm entspricht die Breite der vier Finger ungefähr 10010 %0 = ca. ½ Fingerdicke. Der halbe Kreisumfang hat 3141 %

3141 Umrechnung auf Grade: 117,44 °/00.

180 Aus der nachfolgenden Fig. 3 ist leicht zu erkennen, wie sich der Geländewinkel aus Höhendifferenz und Distanz errechnet:

In der Erdmessung wird ein Höhenunterschied meist mit zu? bezeichnet ( lies « Delta Ha » ).

Obige Gleichung und Fig. 3 gelten nur für kleinere Distanzen, weil wir die runde Erdoberfläche dabei durch eine Ebene ersetzt haben, während Fig. 1 bereits den durch die Erdkrümmung verzerrten, scheinbaren Geländewinkel zeigt.

Ableitung der Formel Wenden wir in Fig. 4 auf das rechtwinklige Dreieck ABC den Satz von Pythagoras an, wonach das Quadrat über der Hypothenuse AC gleich ist der Summe der beiden Quadrate über den Katheten BA und BC, so ist offenbar wo R = Erdradius, im Mittel = 6370 km d — Horizontaldistanz BA in km h = gesuchter Betrag der Erdkrümmung für das Objekt A, in km.

Dabei müssen wir uns allerdings bewusst sein, dass wir schon beim Ansatz obiger Gleichung etwas gemogelt haben, indem wir anstatt dem richtigen d, das längs dem Kreisbogen BF zu messen wäre, einfach die Länge der Tangente BA genommen haben. Da aber die Strecke d im Verhältnis zum Erdradius sehr klein ist, zeigt eine Kontrollrechnung, dass der Fehler für unsere Verhältnisse nicht einmal ein hundertstel Prozent ausmacht. Es dürfte die Distanz d aus Sichtbarkeitsgründen kaum je 250 km ( Bernina—Mont Blanc ) überschreiten. Der Zentriwinkel wird dann az¾¾y = 39 °/00 oder 2X\±°. Diese Verhältnisse zeigt Fig. 5 im Maßstab 1:100 000 000.

Im übrigen gibt uns die Formel I den genauen Wert für h; sie ist jedoch sehr unpraktisch zum Rechnen. Man wird damit trotz Logarithmen oder Quadratzahltafeln nur sehr schlecht fertig. Wer's probiert, wird gleich merken, dass der Ausdruck ]/i?2 + d2 sehr nahe an R kommt.

Also versuchen wir eine Formel zu erhalten, die wir mit dem Rechenschieber oder sogar im Kopf auflösen können. Wir fanden unter I ( R + h)2 = R2 + d2 oder ausmultipliziert: R2 + 2R h + h2 = R2 + d2 Streichen wir beidseitig das R2 weg, so bleibt ( II2 In dieser, für unser gesuchtes h immer noch quadratischen Gleichung II entdeckt jedoch der praktische Mathematiker sogleich mit Behagen, dass das Glied h2 gegenüber 2R h sehr klein ist; es beträgt z.B. für die oben zitierte Maximaldistanz 24 gegenüber 62 500. Für alle Fälle, wo « /klei-ner als 250 km ist, wird die Differenz relativ noch grösser. Daher dürfen wir uns ohne weiteres gestatten, das Glied h2 einfach wegzulassen. Dann erhalten wir aus II d2

2R-h=d2 oder halso 2J\.

wo D = 2R = mittlerer Erddurchmesser = 12 740 km d = Distanz in km.

cm ) km Wir wollen diesen Wert h den Erdkrümmungsdefekt nennen.

Der Mathematiker ersieht aus dieser Formel sofort, dass wir nur den Kreis durch einen sich genau anschmiegenden Parabelbogen ersetzt haben, mit dem sich viel bequemer rechnen lässt. ( Der Radius des « Berührungskreises » im Scheitel der Parabel ist = Rl ) Machen wir die Kontrolle, wie gross der dabei begangene Fehler ist, so konstatieren wir mit Genugtuung, dass er für unsere praktischen Maximaldistanzen bis 250 km nicht ganz ein Prozent erreicht. Unsere Resultate sind also im Mittel vielleicht um ca. 1/20 % zu klein. Daher können wir beruhigt zur praktischen Anwendung übergehen und rechnen.

Einige Beispiele 1. Wir schwimmen beim Bürkliplatz in Zürich. Wegen der seitlichen Biegung des Sees sind die am weitesten entfernten Häuser am See, die man noch sehen kann, diejenigen von Horgen. Wir fragen uns, wie weit der tiefste Sehstrahl in Horgen über dem Seespiegel durchgeht, d = 12,5 km h = 12,5x12,5 ~1274CT = 0,0122 km 12,2 m.

Der Schwimmer kann also das am Hafen von Horgen stehende historische Sust-Haus unmöglich sehen.

Könnte man nach Rapperswil sehen ( d = 26 km ), so wären mit h = 53 m wohl nur die Türme des Schlosses sichtbar.

Geht unser Schwimmer nach Bregenz und sucht in Richtung Konstanz nach dem Münsterturm, so tut er dies vergebens. Denn es wird mit d = 50 km, h = 196 m!

Klettert er jedoch auf die Quaimauer hinauf, wobei ho = 5 m sein möge ( Fig. 7 ), so findet man die Kimmdistanz ( Berührungspunkt des Sehstrahls mit dem See ) durch Umkehrung unserer Formel, also:

d =yho-D0,005 X 12740 = 8 km.

Daher bleibt für d1 = 50—8 = 42 km, und unser hx wird 42x42 12740 = 0,138 km.

Es wird trotzdem eine Enttäuschung sein, denn der sonst so weithin sichtbare Münsterturm von Konstanz bleibt unter der Kimm. Er ist niemals 138 m hoch.

2. Wir stehen auf dem Gipfel des Rheinwaldhorns. H = 3405 m.

a ) Die Dufourspitze mit H = 4637 m ist gut sichtbar, und wir messen aus der Übersichtskarte d = 121 km. Daraus ergibt sich h1,15 km = 1150 m.

D1Z/4U Fast unglaublich scheint diese Zahl, die besagt, dass uns also die Dufourspitze, vom Rheinwaldhorn aus gesehen, volle 1150 m tiefer erscheinen muss als wenn wir anstatt auf der Erdkugel auf einer ebenen Welt wohnen würden, wie sie sich etwa die Griechen vorgestellt haben. Sein schein- barer Geländewinkel ist also um121 = 9,5 Oi00 kleiner, als er in einer ebenen Welt beobachtet würde.

Anstatt dass der Gipfel um AH = 4637—3405 = 1232 m oder rund 10über unserem scheinbaren Horizont erscheint, beobachten wir, als wäre er nur 1232—1150 = 82 m höher als unser 82 Standort, als unsere Höhenhülle. Wir messen die Spitze effektiv mit einem scheinbareny = 2/3 °/00 über unserem scheinbaren Horizont. Die gestrichelte Linie in Fig. 8 zeigt Monte Rosa in der ebenen Welt.

b ) Da es so ausserordentlich sichtiges Wetter ist, sehen wir uns auch gleich nach dem Mont Blanc um. H = 4807 m. Aus d = 184,5 km errechnen wir seinen Erdkrümmungsdefekt zu 184,5x184,5 = 2,67 km! Wir finden ferner aus der Karte, dass er über dem Grat nördlich des h 12740 Fletschhorns, bei Pt. 3775, erscheinen müsste. Bis dorthin ist unser Blick frei. Für diesen Grat in 88 5 x 88 5 d — 88,5 km Entfernung wird, weil viel näher als Mont Blanc, h0,614 km. Um zu beurteilen, ob wir Mont Blanc sehen können, müssen wir für diesen Grat sowie für Mont Blanc die scheinbaren Geländewinkel ermitteln. Ist der Wert für Mont Blanc grösser als für den Grat, so wird er darüber erscheinen; ist er hingegen kleiner, so wird uns die weisse Kuppe verborgen bleiben. Es ist in unserem Beispiel sehr interessant, gerade für beide Fälle zu rechnen:

1. für eine ebene Welt ( richtig bei kleinen Distanzen ); 2. für unsere kugelige Erde, d.h. so wie die Verhältnisse effektiv sind.

1.

Ebene Welt 2.

Runde Welt Adula-Mont Blanc AH = 1402 m d = 184,5 km7,2°/oo AH = 1402—26701268 m d = 184,5 km scheinbarer6,8 °/M Adula-Fletschhorngrat AH = 370 m d = 88,5 km4,2% Der Mont Blanc überragt also den Grat um 7,2—4,2 = 3 °/oo und sollte daher sichtbar sein.

AH = 370—614244 m d88,5 km scheinbarer2,7 0/- Der Mont Blanc bleibt um 6,8—2,7=4,1 %0 unter dem Grat; er ist also nicht sichtbar.

Dies wegen seinem grossen Erdkrümmungsdefekt von h = 2670 m, infolge der viel grösseren Distanz.

Im Vertikalschnitt gesehen, sieht dies ungefähr so aus:

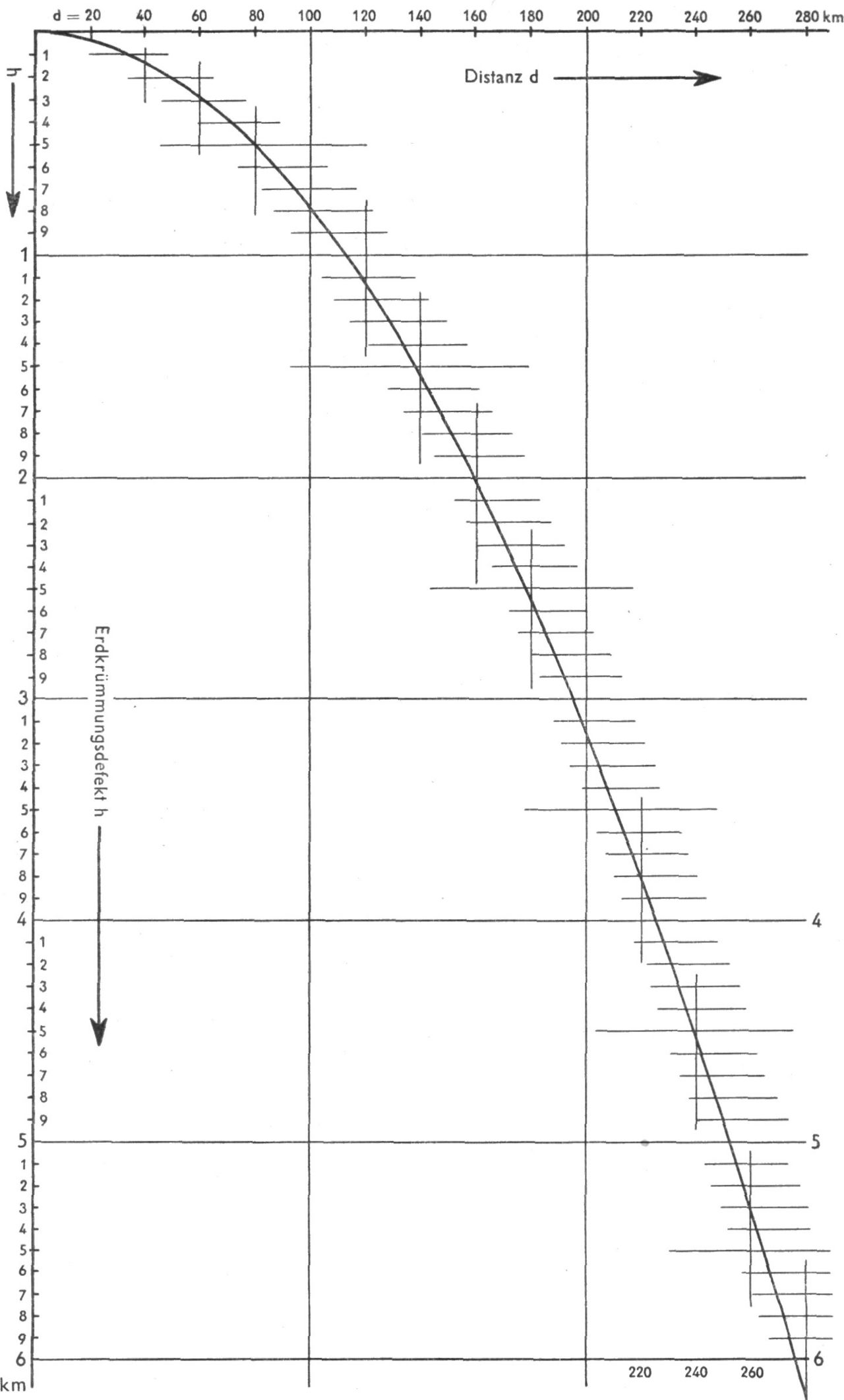
72 Damit man den Erdkrümmungsdefekt h, auch wenn man ihn vom Rechenschieber mit einer einzigen Einstellung erhält, nicht stets rechnen muss, empfiehlt es sich, für diesen Wert ein Graphikon aufzustellen, aus dem man zu jedem d das entsprechende h entnehmen kann. Dies ist für unsere Verwendung genau genug.

d(km ) d- A ( km ) 20 400 0,0314 30 900 0,0705 40 1600 0,1255 50 2 500 0,1960 60 3 600 0,2820 70 4 900 0,3850 80 6 400 0,5010 90 8 100 0,6350 100 10 000 0,7850 d(km ) d* h ( km ) 120 14 400 1,130 140 19 600 1,540 160 25 600 2,010 180 32 400 2,540 200 40 000 3,140 220 48 400 3,790 240 57 600 4,510 260 67 600 5,300 280 78 400 6,170 Den singulären Wert von h = 1000 m erhält man natürlich für

13 Die Alpen - 1957 - Les Alpes193 Aus dieser Kurve herausgelesen sind nachfolgende Werte, die vielleicht allgemeines Interesse haben:

rf(km ) A ( m ) Betrag in °/0«. um den der Berg infolge Erd- krümmung niedriger erscheint Genf—Mont Blanc

69 69 112 36 90 122,5 59 5 375 375 985 102 635 1175 280 5,4 5,4 8,8 2,8 7,0 9,6 4,7 Zürich—Tödi.

Mailand ( Dom)-Monte Rosa

Titlis-Finsteraarhom

Titlis-Dom

Säntis—Finsteraarhorn.....

Säntis—Tödi

Säntis—Chasserai.....

175,5 69 147 5 2400 375 1700 13,7 5,4 11,5 Chasserai—Jungfrau....

Chasserai—Mont Blanc...

Chasseral-Bernina

235 4330 18,4 Forch-Blümlisalp

114 240 276 1020 4510 6000 9,0 18,8 21,7 Feldberg-Mont Blanc

Ballon d' Alsace-Bernina

3. Nachdem wir auf dem Rheinwaldhorn so interessante Beispiele fanden, begeben wir uns auf den Piz Bernina, in der Hoffnung, dort noch grössere Distanzen auswerten zu können. H = 4052 m.

a ) Visieren wir zuerst wieder die Dufourspitze an. In dieser Richtung liegen als nächste Punkte der Scerscen und Piz Roseg. Um sicher zu sein, dass uns diese beiden keinen Streich spielen, rechnen wir darauf die $ aus und finden:

__noScerscenr130 °/M u,6 __112Piz RosegTr53 °/00 Daraus erhält man den Eindruck, dass die Sicht frei sei.

Dufourspitze H = 4637 m d = 166 km AH585 m aus Graphikon h = 2175 m Differenz1590 m Scheinbarer9,6 °/00.

Der Monte Rosa muss uns somit erscheinen, wie es in der ebenen Welt ein Berg von 4637—2175 = 2462 m Meereshöhe tun würde, und befindet sich 9,6 °/00 unter dem scheinbaren Horizont. Er wird uns also, von der Bernina aus gesehen, durch seine Höhe gar nicht beeindrucken; er wird dies nur tun können im Vergleich mit seiner Umgebung und durch die Luftperspektive. ( Die Farbe weit weg liegender Schneegebirge zeichnet sich durch einen eigentümlichen Rosaschimmer aus. ) b ) Ziehen wir auf unserer Übersichtskarte den Sehstrahl nach dem Mont Blanc, so konstatieren wir, dass er genau durch den Gipfel des Rimpfischhorns geht. Dieses könnte unserer Sicht leicht gefährlich werden!

Mont Blanc H = 4807 m d = 243 km AH755 m aus Graphikon h = 4600 m!

Differenz3845 m Scheinbarer15,8 °/oo Rimpfischhorn H = 4202 m d = 162 km AH150 m aus Graphikon h2075 m Differenz1925 m Scheinbarer11,9Es zeigt sich also auch hier, dass der Mont Blanc nicht sichtbar ist, indem er sich 15,8—11,9 = 3,9 " /oo tiefer als das Rimpfischhorn befindet.

Da fast 4 °jm in der Senkrechten bei der Flachheit der Panoramen einen sehr erheblichen Betrag bedeuten, dürfte vom ganzen Mont-Blanc-Massiv überhaupt nichts erblickt werden können.

Wir wollen noch rasch sehen, ob in einer ebenen Welt der Mont Blanc das Rimpfischhorn für den Berninabeobachter überragen würde. Die Beobachtungsgeländewinkel geben Auskunft:

Mont Blanc = 7553,1 « /„e0,9°/oo 243 + 150 162 & Rimpfischhorn = Mont Blanc würde also das Rimpfischhorn mit 2,2 °/00 ordentlich überragen.

4. Ein denkbar günstiger Standort für unsern Beobachter wäre zweifellos der Generoso, weil sich dort Bahn und Wirtschaft befinden, so dass meine Rechnungen auf angenehmste Weise nachkontrolliert werden könnten. Dass die Dufourspitze dort sichtbar ist, weiss jedes Kind. Sie ist 90 km entfernt und erleidet daher einen Erdkrümmungsschwund von 635 m.

Anders steht es wieder mit unserem zweiten Liebling, dem Mont Blanc. Der Sehstrahl dorthin bleibt hängen an einem Buckel bei den « Colle delle Pisse », H = 3202 m, der sich in einer Distanz von 90 km, 6,3 km direkt südlich der Dufourspitze, befindet.

GenerosoH = 1705 m Mont Blanc H = 4807 m d = 168 km AH3105 m aus Graphikon h2220 m Differenz885 m Scheinbarer885 168 Colle delle Pisse H = 3202 m AH1497 m h635 m